Phase Extraction
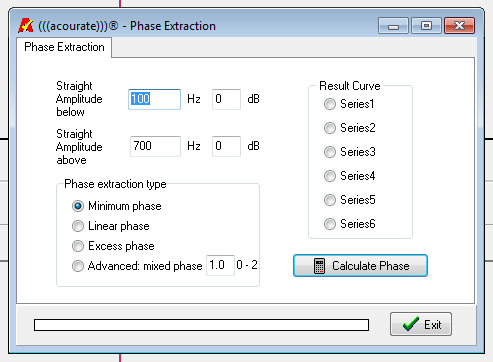
Description:
Below the lower limit and above the upper limit specified frequency, the frequency response of the loaded curve is made flat.
Options:
- Minimum phase: This option is used to calculate the unique impulse which has the specifed frequency response and is Minimum Phase. A minimum phase filter has the smallest possible group delay at any given frequency (consistent with producing the required overall frequency response), and hence the smallest signal latency, but the group delay may not be constant at all relevant frequencies. The minimum phase impulse has no pre-ringing but may have post-ringing. The location of the pulse peak is usually at or near the first sample of the filter.
- Linear phase: This option is used to calculate a filter (impulse) which has the specified frequency response with a constant group delay at all frequencies. The price for a constant group delay is that the absolute group delay is large. The large constant delay may not matter if listening to audio, but needs to be taken into account if audio is live or needs to be synchronized with video. The impulse is symmetric, with the pulse peak located in the center of the filter. Accordingly, the delay is equal to half the filter length / sampling rate (for a filter 65536 samples long at 44100 Hz, the delay is 32768/44100 or about 0.74 seconds). The build up of the pulse before the pulse peak is called “pre-ringing” which in some cases may cause audible artifacts.
- Excess phase: This option calculates a filter with constant 0 dB frequency response but which incorporates any group delay in the input curve in excess of that which the minimum phase component of that curve would produce. Because of the flat amplitude response, such a filter is often called an “All Pass” filter. A typical impulse response can be separated into the minimum phase component and the excess phase component. Convolving the two components reproduces the original pulse.
- Advanced mixed phase: With this option, while maintaining the frequency response, any phase curve between minimum phase (0), Linear Phase (1) and maximum phase (2) are calculated. The parameter can also be in between, for example, 0.159. Possible application: a steep low pass filter can be created between minimum phase (only post-ringing) and linear phase (same pre- and post-oscillation) can be set, with some pre-ringing but more post-ringing. (There is no free lunch: zero ringing is unachievable with systems of finite frequency response!)
Use:
The choice of correction filter for a mixed-pulse response may be due principally to the amount of acceptabe delay. For pure audio reproduction this usually does not matter. In the case of video or live music, a large delay may not be acceptable. Here the shortest lead time is achieved with a minimum phase correction filter. But no excess phase is corrected.
A limited band of frequency response can be used for a correction with this function with the frequency response information discarded above or below the selected spectrum (that is, the frequency response output of this funtion is a horizontal straight line below the lower limit and above the higher limit). This function is required, for example to use a near-field recording of frequency response of a speaker driver to linearize digital crossovers. It allows the creation of a correction filter to correct the frequency response of the speaker driver only within a desired frequency band.
Example:
In the following example, a correction filter is desired which corrects only the bass up to about 150Hz. For this purpose Room Macro 1-3 are used to obtain the inverse of the pulse responses from which the correction filters are created. The inverse pulse responses are saved by Room Macro 3 in the working directory under the file name Pulse48Linv.dbl or Pulse48Rinv.dbl. After execution of Macro 3 to delete all curves from the view, load the two inverse curves in curve 1 and curve 2, and zoom in on the relevant frequency range:
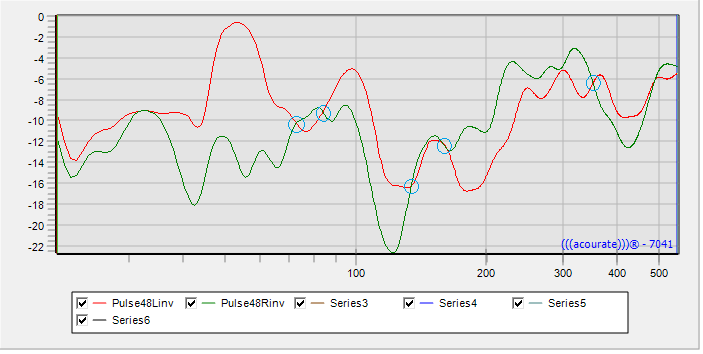
In this case it is important that the uncorrected range of frequencies above approximately 150hz have the same gain applied by the filter, otherwise it will affect the balance of the channels. So for the next step there are two possibilities: either you find an intersection of the two curves around 150hz, or you set slightly different high frequency limits for the correction in the two channels in order to get the same gain. What matters is that the two amplitudes are equal at the high limit of correction.

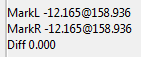
In this example, we have zoomed into the intersection at about 150HZ and clicked the exact point of intersection with the left mouse button. Then you get on the right side of the program window, the frequency at which the mark has been set.

Now activate the curve 1 on the radio button and select TD Functions> Phase Extraction. Select Minimum Phase as Room Macro 4 will be used later to correct excess phase. The frequency response is to be straightened from 159Hz, and the result is loaded into curve 3. Similarly, the result of Phase Extraction of curve 2 is loaded into curve 4.
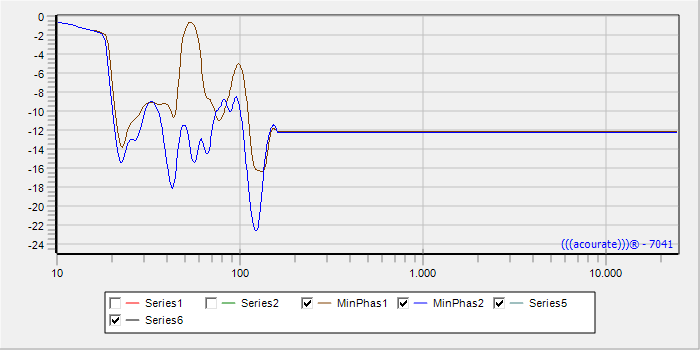
After deleting the original curves you get the following picture. The two new files still must be saved with the name of the old inverse (or Pulse48Linv.dbl Pulse48Rinv.dbl). After that you can create a filter with Room Macro 4.
